PPT Hamiltonian Formulation of General Relativity PowerPoint

General relativity treats space and time on the same footing, that is not what is done in Hamiltonian formulations. Therefore, in order to discuss general relativity in a Hamiltonian fashion, one needs to break that equal footing. This requires a space-time splitting, since only time derivatives are transformed to momenta but not space derivatives.

(PDF) New Hamiltonian Formulation of general relativity

for any Hamiltonian formulation of General Relativity (GR); (ii) the canonical treatment unavoidably breaks the symmetry between space and time in GR and the resulting algebra of constraints is not the algebra of four-dimensional diﬀeomorphism; (iii) according to some authors this algebra allows one to derive only spa-

(PDF) The Principle of Covariance and the Hamiltonian Formulation of

Let us mention that from the very beginning the complexity of General Relativity inspired the search for suitable parametrizations to solve various problems. There are other examples of constructing Hamiltonian dynamics of General Relativity, for instance, the formulation by Faddeev in his work devoted to gravitational energy [4]. He made use of

(PDF) Principles of Hamiltonian formulation(s) of the metric General

A conventional wisdom often perpetuated in the literature states that: (i) a 3 + 1 decomposition of spacetime into space and time is synonymous with the canonical treatment and this decomposition is essential for any Hamiltonian formulation of General Relativity (GR); (ii) the canonical treatment unavoidably breaks the symmetry between space and time in GR and the resulting algebra of.

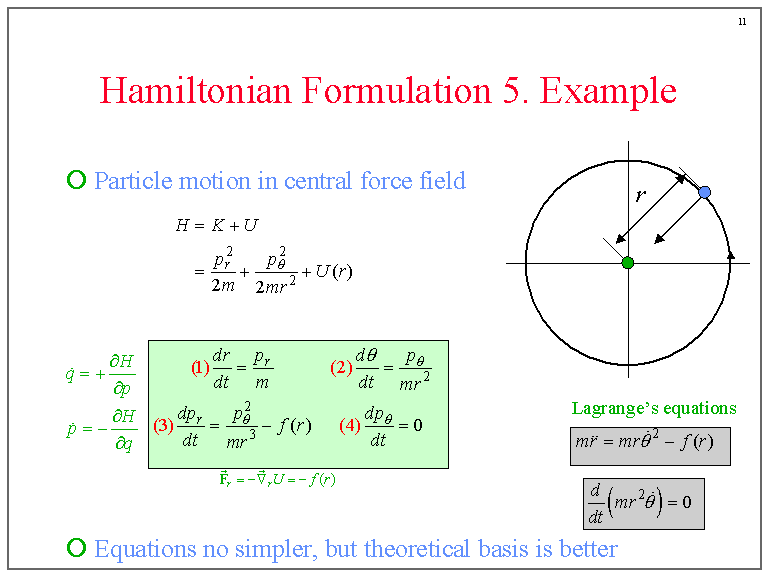
Hamiltonian Formulation 5. Example

Chapter1. Introduction 3 BianchiIX-Maxwellsystem. InSection6.3,westudyafree&masslessclassicalscalar ﬁeld coupled to the Bianchi IX-Maxwell system in the Hamiltonian formalism and

PPT Hamiltonian Formulation of General Relativity PowerPoint

Summary. As we will see throughout this book, Hamiltonian formulations provide important insights, especially for gauge theories such as general relativity with its underlying symmetry principle of general covariance. Canonical structures play a role for a general analysis of the systems of dynamical equations encountered in this setting, for.

Hamiltonian Formulation of General Relativity M O Katanaev

We give a pedagogical introduction to the Hamiltonian formalism of general relativity at an advanced undergraduate and graduate levels. After covering the mathematical pre-requisites as well as the $3+1$-decomposition of spacetime, we proceed to discuss the Arnowitt-Deser-Misner (ADM) formalism (a Hamiltonian approach) of general relativity. Then we proceed to give a brief but self-contained.

Hamiltonian analysis of the BFCG formulation of general relativity

The Arnowitt-Deser-Misner ( ADM) formalism (named for its authors Richard Arnowitt, Stanley Deser and Charles W. Misner) is a Hamiltonian formulation of general relativity that plays an important role in canonical quantum gravity and numerical relativity. It was first published in 1959.

Figure 1 from Hamiltonian Analysis In New General Relativity Semantic

Hamiltonian Formulation of General Relativity The formulation discussed here is called the ADM (Arnowitt-Deser-Misner) formulation and was ﬁrst proposed in 1962. In some literature it is also referred to as the Cauchy or 3+1 formulation, the reasons which will soon become obvious. It has found much success in the area of numerical relativity

(PDF) REFORMULATION OF LAGRANGIAN & HAMILTONIAN IN THEORY OF RELATIVITY

The usual approach to treating general relativity as a ﬁeld theory is based on the La-grangian formulation. For some purposes (e.g. numerical relativity and canonical quan-tization), a Hamiltonian formulation is preferred. The Hamiltonian formulation of a ﬁeld theory, like the Hamiltonian formulation of particle mechanics, requires choosing.

PPT Hamiltonian Formulation of General Relativity PowerPoint

It is the purpose of this chapter to develop the Hamiltonian formulation of general relativity, which will serve as the starting point for quantization in Chapters 5 and 6.In the present section, we shall derive it directly from the algebra of surface deformations (Section 3.3), while in the next section, it will be recovered from the Einstein-Hilbert action through a 3 + 1 decomposition.

PPT Hamiltonian Formulation of General Relativity PowerPoint

on developing the mathematics required for the two approaches towards general relativity, namely the Lagrangian formulation as well as the Hamiltonian formulation. In particular, Sec-tion2.2provides a brief but rigorous derivation of Einstein field equations using the Einstein-Hilbert action in the Lagrangian formulation.

PPT Hamiltonian Formulation of General Relativity PowerPoint

Hamiltonian formalisms provide powerful tools for the computation of approximate analytic solutions of the Einstein field equations. The post-Newtonian computations of the explicit analytic dynamics and motion of compact binaries are discussed within the most often applied Arnowitt-Deser-Misner formalism. The obtention of autonomous Hamiltonians is achieved by the transition to Routhians.

PPT Hamiltonian Formulation of General Relativity PowerPoint

The Hamiltonian formulation of general relativity in terms of Ashtekar-Barbero variables can be understood as an extension of the ADM phase space along with a change of coordinates on this.

(PDF) Linking the ADM formulation to other Hamiltonian formulations of

An Evolving Spacetime Metric Induced by a 'Static' Source. M. Land. Physics. Symmetry. 2023. In a series of recent papers we developed a formulation of general relativity in which spacetime and the dynamics of matter evolve with a Poincaré invariant parameter τ. In this paper, we apply the…. Expand.